Hier mal wieder ein Rätsel:
gesucht wird die kleinste Zahl, die auf die 7 endet und sich verfünffacht, wenn man die 7 als letzte Ziffer entfernt und als erste Ziffer an den Anfag der Zahl stellt.
Hinweis
Es hilft sich zu überlegen, welche Zahl vor der 7 stehen muss.
Lösung
Die gesuchte Zahl endet auf 7, hat also die Form:
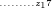
Wobei 
die noch unbekannte vorletzte Ziffer darstellt.
Nach der Umstellung sieht sie so aus:
und weiterhin soll ja gelten:
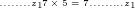
Da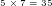 
ist, muß 
gleich 5 sein. Gleizeitg ensteht aber auch ein Übertrag von 3 auf die nächste Stelle. Man erhält so:
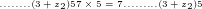
Nun bestimmt man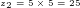 
. So ergibt sich als nächste Ziffer die 8 (durch den Übertrag von 3) und man erhält einen neuen Übertrag von 2:
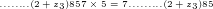
Durch wiederholte Anwendung:
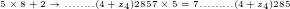
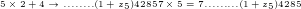
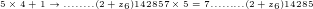
Und letzlich ergibt sich mit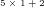 
als nächste Ziffer die 7 und wir haben die Lösung:
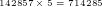
VN:F [1.9.22_1171]
Rating: 1.0/5 (1 vote cast)
